영지식 증명은 어떤 정보를 가지고 있음을 입증하지만 그 정보의 내용은 공개하지 않는 방법을 말합니다. 이미 영지식 증명을 접해봤다면, 알리바바의 동굴 비유를 많이들 떠올릴 것입니다. 그러나 바로 이어지는 수학 용어들의 향연에서 진입 장벽을 느꼈을 것이라 생각합니다. 이 글에선 영지식 증명을 좀더 간단하게 이해할 수 있도록 구슬을 사용한 예시로 설명해보겠습니다.
철수는 두 개의 컵을 가지고 있는데, 각 컵 안에는 5 개의 구슬이 들어 있습니다. 이때, 저울을 사용하지 않고 영희에게 두 컵 안의 구슬 개수가 같다는 것을 입증할 수 있을까요? 물론, 구슬의 개수를 직접 밝히지 않고 말입니다.
Interactive Proof System
상대방과 상호작용하며 반복을 통해 확률적으로 증명하는 방식을 대화형 증명 시스템이라 고 합니다. 한번 이 상황을 대화형 증명 시스템으로 해결해봅시다.
처음에 철수가 가진 컵을 A 컵과 B 컵이라고 합시다. 이때, 필요한 준비물로는 두 개의 추가적인 컵 (C와 D)과 구슬이 필요합니다.
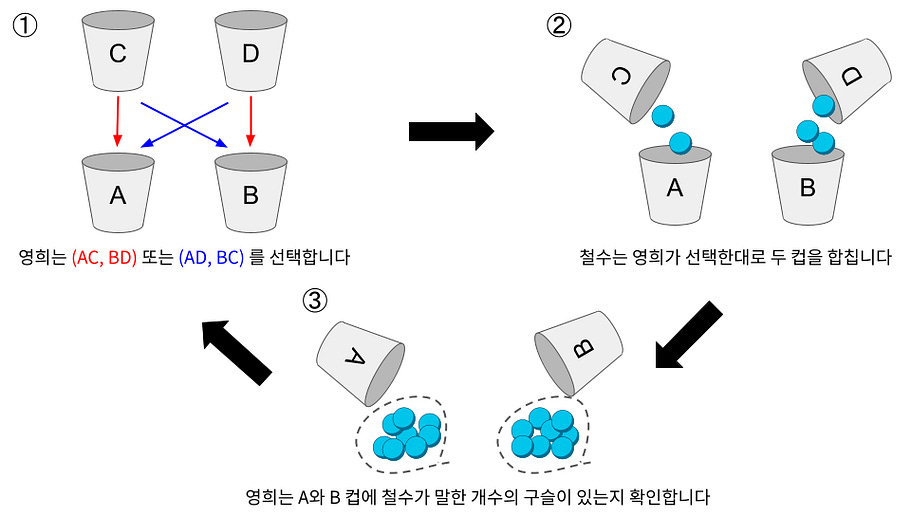
철수는 무작위로 숫자, 예를 들면 3을 선택하고, C와 D 컵에 해당 숫자만큼 구슬을 넣습니다.
다음으로, 철수는 구슬 개수의 합, 이 경우에는 8을 영희에게 알립니다.
영희는 (AC, BD) 또는 (AD, BC) 두 가지 선택지 중 하나를 고릅니다.
그런 다음, 철수는 영희가 선택한대로 두 컵을 합칩니다. 예를 들어, 영희가 (AC, BD)를 선택하면 C 컵의 구슬을 A 컵으로, D 컵의 구슬을 B 컵으로 옮깁니다.
영희는 이제 두 컵에 각각 8 개의 구슬이 있는지 확인합니다.
이후, 1단계로 돌아가 이 과정을 여러 번 반복합니다.
위와 같은 과정을 통해 영희는 철수를 믿을 수 있을까요?
만약 처음에 A와 B 컵에 들어있던 구슬의 개수가 다르다면 철수가 C와 D 컵에 구슬의 개수를 어떻게 조정하더라도 영희가 고른 선택지 (AC, BD) 또는 (AD, BC) 중 하나는 반드시 거짓말이 드러날 것입니다. 즉, 50% 확률로 철수가 거짓말하고 있음이 드러나게 됩니다. 따라서 이 과정을 여러번 반복할수록 철수의 거짓말이 성공할 확률은 50%, 25%, 12.5%, … 0% 에 가까이 낮아지므로 영희는 철수를 믿을 수 있게 됩니다.
이 과정에서 중요하지 않은 정보가 노출되고, 구슬을 컵에서 빼거나 추가하기 어려운 문제점이 있을 수 있지만, 이것은 우리가 디지털 세계에서 다루지 않아도 되는 것이기 때문에 크게 문제되지 않습니다.
Non-interactive Proof System
하지만 대화형 증명 시스템은 실시간 통신이 필요하기 때문에 번거로울 수 있습니다. 그래서 일반적으로 대화형 증명 시스템을 비대화형 증명 시스템으로 변환해서 사용합니다. 그럼 우리도 비대화형 증명 시스템으로 바꿔봅시다.
이번에는 영희를 포함하지 않고 철수만이 증명 과정에 참여합니다. 필요한 준비물로는 두 개의 추가 컵(C와 D), 구슬, 동전 그리고 카메라가 필요합니다.
카메라로 동영상 녹화를 시작합니다.
철수는 무작위로 숫자, 예를 들면 3을 선택하고, C와 D 컵에 해당 숫자만큼 구슬을 넣습니다. 이 때 3개인 것을 동영상을 통해 알 수 없도록 주의합니다.
다음으로, 철수는 구슬 개수의 합, 이 경우에는 8을 카메라에 대고 말합니다.
동전을 던져 결과를 카메라에 보여줍니다.
동전의 결과에 따라 두 컵을 합칩니다. 앞면이 나오면 (AC, BD), 뒷면이 나오면 (AD, BC)가 됩니다.
두 컵에 각각 8 개의 구슬이 있는지 카메라에 보여줍니다.
이후, 2단계로 돌아가 이 과정을 여러 번 반복한 후 동영상 녹화를 종료합니다.
비대화형 증명 시스템과 대화형 증명 시스템의 차이는 무엇일까요? 대화형 증명 시스템에서는 영희가 선택을 하지만, 비대화형 증명 시스템에서는 철수가 동전 던지기를 통해 결과를 만듭니다. 이렇게 하더라도 철수는 결과를 조작할 수 없으며, 영희에게 동영상만 제출하면 증명이 완료되기 때문에 훨씬 편리합니다.
Shuffle using Encryption
또한, 영지식 증명에서 자주 사용되는 암호화를 활용한 섞는 방법도 있습니다. 마찬가지로 예시를 통해 살펴봅시다. 이 경우, 다수의 준비물이 필요합니다. A와 B 컵을 포함하여 총 10개의 컵 쌍 (20 개의 컵), 10 개의 작은 상자, 10 개의 큰 잠금 상자, 그리고 구슬을 준비합니다.
철수는 추가로 준비한 9개의 컵 쌍에 각각 1개, 2개, …, 4개, 6개, …, 10 개의 구슬을 넣습니다. 5개를 제외하는 이유는 이미 A와 B 컵에 5개씩 들어있기 때문입니다.
그런 다음, 철수는 각 컵 쌍을 작은 상자에 넣습니다.
영희는 작은 상자를 큰 잠금 상자에 넣고 잠급니다.
철수는 영희에게 보이지 않게 상자들을 섞습니다.
마지막으로, 모든 상자를 열고, 영희는 각 상자 안의 두 컵에 동일한 구슬 개수가 들어 있는지 확인합니다.
마지막 과정에서 영희는 모든 상자를 열어 (1개, 1개), …, (10개, 10개) 씩 들어있는 컵 쌍을 확인하게 됩니다. 즉, A와 B 컵도 이 10 개의 컵 쌍 중 하나이므로 동일한 구슬 개수가 들어있었다는 사실을 검증할 수 있습니다.
그렇다면 영희는 A와 B 컵에 5개의 구슬이 들어있었다는 것도 알 수 있을까요? 아닙니다. 상자를 섞어놓았기 때문에 영희는 A 와 B 컵의 위치를 알지 못합니다. 오로지 1개에서 10개 사이라는 사실만 알 수 있습니다.
혹시 누군가는 다음과 같은 질문이 떠올랐을 것입니다. “왜 상자를 잠근 후 섞어야 할까요? 그냥 열어서 섞어도 되지 않나요?” 그에 대한 답은, 상자를 섞을 때 철수가 몰래 상자를 열어서 내용물을 바꿀 수 있는 가능성을 방지하기 위해서입니다. 이렇게 함으로써 증명 과정을 온전히 믿을 수 있게 만듭니다.
마치며
영지식 증명은 정보를 입증하는 방법 중 하나로, 두 가지 중요한 기능인 영지식과 간결성을 결합한 기술입니다. 지금까지는 영지식에만 초점을 맞추어 설명해보았습니다. 그러나 간결성은 작업 비용을 낮추기 위한 매우 중요한 기능입니다. 이 간결성에 대해서도 기회가 된다면 자세히 다루어 보도록 하겠습니다.
마지막으로, 여러분들도 아래 명제들을 증명할 방법을 창의적으로 생각해보는 건 어떨까요?
A 컵에 들어있는 구슬의 개수가 B 컵보다 많다.
여러 개의 컵 중에서 가장 많은 구슬을 가진 컵에는 10개의 구슬이 들어있다.
여러 개의 컵에 들어있는 구슬의 합이 100개이다.
면책조항
본 저작물은 정보 전달 목적으로만 제공되며, 투자 조언이 아닙니다. 저자는 제공되는 정보의 정확성을 위해 많은 노력을 기울였음에도 불구하고 정보의 정확성이나 완벽성에 대해, 명시적이거나 묵시적으로든 약속 또는 보증하지 않으며, 이에 대해 법적 책임을 지지 않습니다. 또한 저작물을 투자 판단 등의 의사 결정에 활용함으로 인해 발생할 수 있는 어떠한 종류의 손해에 대해서도 책임을 지지 않습니다.